A watertight bulkhead is 8m high and is supported by vertical stiffeners 700mm apart, connected at the tank top by brackets having 10 rivets 20mm diameter. The bulkhead is flooded to its top edge with sea water. Determine: (a) Shearing force at top of stiffeners, (b) Shear stress in the rivets, (c) Position of zero shear.
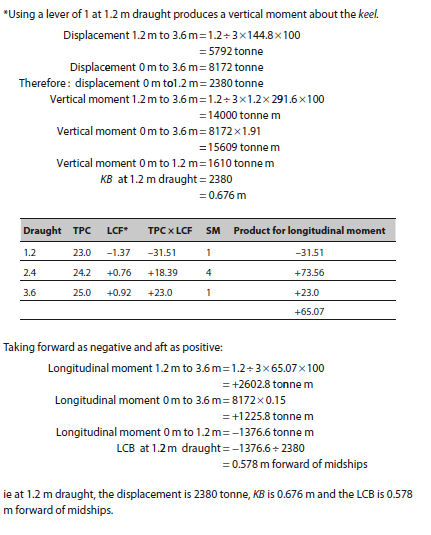
A vessel, when floating at a draught of 3.6 m has a displacement of 8172 tonne, KB 1.91 m and LCB 0.15 m aft of midships. From the following information, calculate the displacement, KB and position of the LCB for the vessel when floating at a draught of 1.2rn
The ½ ordinates of a water plane at 15m intervals, commencing from aft, are 1, 7, 10.5, 11, 11, 10.5, 8, 4 and 0 m. Calculate:
i. TPC
ii. Distance of the centre of flotation from midships
iii. Second moment of area of the water plane about a transverse axis through the centre of flotation.
IF YOU ARE NOTICING ANY ERROR KINDLY COMMENT BELOW
Solution
½ ordinate | SM | Product of area | lever | Product for 1st moment | lever | Product for 2nd moment |
1 | 1 | 1 | +4 | +4 | +4 | +16 |
7 | 4 | 28 | +3 | +84 | +3 | +252 |
10.5 | 2 | 21 | +2 | +42 | +2 | +84 |
11 | 4 | 44 | +1 | +44 | +1 | +44 |
11 | 2 | 22 | 0 | 0 | 0 | 0 |
10.5 | 4 | 42 | -1 | -42 | -1 | +42 |
8 | 2 | 16 | -2 | -32 | -2 | +64 |
4 | 4 | 16 | -3 | -48 | -3 | +144 |
0 | 1 | 0 | -4 | 0 | -4 | 0 |
∑m = 190 | ∑m1 = +52 | ∑m2 = +646 |
TPC = (Aw x density of water ) / 100
= (1900 x 1.025) / 100
= 19.475
ii)Distance of the centre of flotation from midships = (h x product of first moment) / product of area
X = (15 x +52) / 190
X = 4.11 m towards aft (As value is +ve)
iii) Second moment about midship Im = (2/3) x h3 x Product of 2nd moment
= (2/3) x 153 x 646
= 1453500 m4
Second moment of area about centroid = Im - (Aw x X2)
= 1453500 - (1900 x 4.112)
= 1421405 m4
A 6m model of a ship has a wetted surface area of 7m2 and when towed in fresh water at 3knots has a total resistance of 35 N. Calculate the effective power of the ship, 120 m long, at its corresponding speed. n=1.825. f from formula SCF=1.15
A ship 150m long and 8.5m draught has a rudder whose area is one sixtieth of the middle-line plane and diameter of stock 320mm. Calculate the maximum speed at which the vessel may travel if the maximum allowable stress is 70 MN/m? the centre of stock 0.9m from the centre of effort and the maximum rudder angle is 35 degrees.
A ship 85 m long displaces 8100 tonne when floating in seawater at draughts of 5.25 m forward & 5.55 m aft. TPC 9.0, GML 96 m, LCF 2 m aft of midships. It is decided to introduce water ballast to completely submerge the propeller & a draught aft of 5.85 m is required. A ballast tank 33 m aft of midships is available. Find the least amount of water required & the final draught forward.
IF YOU ARE NOTICING ANY ERROR KINDLY COMMENT BELOW
Given
L = 85 m
Δ = 8100 t
df = 5.25 m
da = 5.55 m
TPC = 9
GML = 96m
LCF = 2 m
To find
i) Amount of water required to make draught aft 5.85 m
ii) Final Forward draught
Solution
We know that moment to change trim one cm, MCT1 cm = (Δ x GML) / (100 x L)
= (8100 x 96) / (100 x 85)
= 91.48 t m
We know that trimming moment = mass moved x distance moved
In question it is given that ballast tank is 33 m aft of midship and LCF is 2 m aft of midship.
i) So distance at which water has to be taken = 33 - 2 = 31 m
So trimming moment = m x 31
Change in trim = trimming moment / MCT1 cm
= (31 x m) / 91.48
t = 0.339 x m -----------------------------------------------(1)
We know that bodily sinkage = mass added / TPC
= m / 9
= 0.111 x m -------------------------------(2)
Distance from LCF to aft = (85/2) - 2 (As 85/2 will be mid ship. then 2 m from mid to LCF)
WF = 40.5 m
Change in draught aft = (t / L) x WF
= {(0.339 x m) / 85} x 40.5
= 0.161 x m ------------------------------------------(3)
So new draught aft = old draught + bodily sinkage + change in draught
5.85 = 5.55 + 0.111 m + 0.161 m
5.85 = 5.55 + 0.272 m
0.272 m = 0.3
m = 1.10 = 110 t (Bodily sinkage and change in trim are in cm)
So amount of water required = 110 t
ii) So Distance from LCF to fwd = (85/2) + 2 (As 85/2 will be mid ship. then 2 m from mid to LCF)
FL = 44.5 m
Change in draught forward = - (t / L) x FL
= -{(0.339 x m) / 85} x 44.5
= - {(0.339 x 110) / 85} x 44.5
= - 19.52 cm
So new draught fwd = old draught + bodily sinkage + change in draught
= 5.25 + (0.111 x 110) - 0.195
= 5.25 + 0.122-0.195
= 5.177 m
A ship 160m long and 8700 tonne displacement floats at a waterline with
½ Ordinates | ½ Ordinate3 | SM | Product |
0 | 0 | 1/2 | - |
2.4 | 13.82 | 2 | 27.64 |
5.0 | 125.00 | 3/2 | 187.5 |
7.3 | 389.02 | 4 | 1556.08 |
7.9 | 493.04 | 2 | 986.08 |
8.0 | 512.00 | 4 | 2048.00 |
8.0 | 512.00 | 2 | 1024.00 |
7.7 | 456.53 | 4 | 1826.12 |
5.5 | 166.38 | 3/2 | 249.57 |
2.8 | 21.95 | 2 | 43.9 |
0 | 0 | 1/2 | - |
TOTAL | 7948.9 |
A ship 120m long displaces 10500 tonne and has a wetted surface area of 3000m2 . At 15 knots the shaft power is 4100KW, propulsive coefficient 0.6 and 55% of the thrust is available to overcome frictional resistance; calculate the shaft power required for a similar ship 140m long at the corresponding speed. ∫ = 0.42 and n = 1.825
An oil tanker 160m long and 22m beam floats at a draught of 9m in seawater. Cw is 0.865. The midships section is in the form of a rectangle with 1.2m radius at the bilges. A midships tank 10.5m long has twin longitudinal bulkheads and contains oil of 1.4m3/t to a depth of 11.5m. The tank is holed to the sea for the whole of its transverse section. Find the new draught
